The Prolog puzzle presented involves arranging members of the Fellowship from "The Lord of the Rings" in a specific order based on given constraints. Here’s a step-by-step description:
Objective
You need to determine the walking order of seven characters: Aragorn, Frodo, Sam, Merry, Pippin, Gimli, and Legolas.
Given Constraints
Aragorn walks before Pippin. Aragorn must come at some position earlier than Pippin. Frodo walks next to at least one other Hobbit. Frodo must be adjacent to either Sam, Merry, or Pippin. Sam walks next to at least one other Hobbit. Sam must also be adjacent to either Frodo, Merry, or Pippin. Gimli walks ahead of Legolas. Gimli must come at some position earlier than Legolas. Merry walks next to Pippin. Merry and Pippin must be directly adjacent in either order. Frodo walks after Aragorn. Frodo must come at some position later than Aragorn.Key Definitions
Order: A list of seven elements representing the walking order of the Fellowship members. Example: [aragorn, frodo, sam, merry, pippin, gimli, legolas]. before/3: A predicate that checks if one character (X) appears before another (Y) in a list (Order). after/3: A predicate that checks if one character (X) appears after another (Y) in a list (Order). It uses the before/3 predicate to establish this relation. hobbit_neighbor/2: A predicate that checks if a character is next to at least one Hobbit in a list (Order). Hobbits include Frodo, Sam, Merry, and Pippin. next_to/3: A predicate that checks if two characters are adjacent in a list (Order).Solution Mechanism
The fellowship_order/1 predicate defines the order and enforces all the constraints using the helper predicates. The list Order is constrained to have exactly the seven members of the Fellowship. The member/2 predicate ensures that all characters are included in the Order. The constraints (before/3, after/3, hobbit_neighbor/2, next_to/3) enforce the relative positions and adjacency as specified.Query
To find the correct order, you can query:
?- fellowship_order(Order).This will produce an Order that satisfies all the given constraints.
Summary
This puzzle requires using logical relations to determine the correct sequence of characters while adhering to the given positional constraints. The use of predicates like before/3, after/3, hobbit_neighbor/2, and next_to/3 helps in logically deducing the valid walking order of the characters.
Fellowship of Prolog
2024-06-25
Logic programming with Prolog can be a very effective way to find solutions to a number of problems. Within Prolog one can define a program by describing it with facts (that represent what we know), rules (that show how to derive new knowledge) and queries (that describe what we would like to know). By using queries on a knowledge base of facts and rules we can solve a variety of problems in many domains.
This approach is quite powerful, but unfortunately Prolog as a programming language is often overlooked. One of the reasons for this is that it can be quite difficult for people without (logic) programming knowledge to break down problems into such terms. Even with experience in Prolog this process can be quite time consuming.
Large Language Models (LLMs), such as Chat-GPT, can provide an interesting way to tackle this issue. In this article I will aim to show how Chat-GPT (or another LLM) could help create and use Prolog programs to solve problems. For this I will be using "Lord of the Rings" themed logic puzzles.

Characters from the Fellowship of the Ring walking in a single line. This is the basic setup for the logic puzzles used in this article.
Let's say we want to describe a situation in which the members of the Fellowship of the Ring are walking down a narrow path. The path is so narrow that no one can walk side by side. Each Fellowship member can only walk in a single line, one after another. The puzzles are based on the idea that given a number of conditions we would like to know in which order the members of the Fellowship are walking.
First let's start off with a small number of conditions to show off the approach. We assume that only three members of the Fellowship are walking: Legolas, Gimli and Frodo. Our restrictions are that Legolas has to walk before Gimli and Gimli must be next to Frodo (this is the reverse order of what it can be seen in the above figure).
In order to model this puzzle with Prolog, first we need to define the notion of the "single line order" that the Fellowship is walking in. In addition we need to define what terms such as before, ahead, etc mean within the context of this puzzle in Prolog. For one well versed in Prolog this can be a pretty routine task but in this case let's assume little to no Prolog knowledge for the person that aims to solve this puzzle. Instead we can ask Chat-GPT to come up with a translation of this problem to Prolog code.
The Prolog code that we use in this article could likely be run with any number of Prolog implementations, such as SWI Prolog. For this article we generate code to use with Tau prolog. The benefit of using Tau prolog is that it can run in the browser and it has an online sandbox available where code can be run without any installation. If one wants to follow along without any setup I highly recommend using this sandbox.
To create the Prolog code for the simplified version of the puzzle we ask Chat-GPT the following question:
"Can you write an example with tau prolog of a logic puzzle in which 3 members of the fellowship need to walk in a single line. Legolas has to be before Gimli and Gimli must be next to Frodo?"
to which Chat-GPT gives us the code:
% Load necessary library
:- use_module(library(lists)).
% Define the predicate to find the order
fellowship_order(Order) :-
Order = [_, _, _], % There are three positions to fill.
member(legolas, Order),
member(gimli, Order),
member(frodo, Order),
before(legolas, gimli, Order),
next_to(gimli, frodo, Order).
% Helper predicate to check if X is before Y in the List
before(X, Y, List) :-
nth0(IndexX, List, X),
nth0(IndexY, List, Y),
IndexX < IndexY.
% Helper predicate to check if X is next to Y in the List
next_to(X, Y, List) :-
( nth0(IndexX, List, X),
nth0(IndexY, List, Y),
abs(IndexX - IndexY) =:= 1
).
% Example query to find the order
% ?- fellowship_order(Order).
From this small example we can see the general outline of how such a logic puzzle can be solved with Prolog. Although we are not going to describe in detail the full syntax and semantics a Prolog program, as there are some excellent introductions on this subject, we are going to briefly go over some concepts.
A Prolog program is a knowledge base in which predicates, such as facts and rules, describe the domain. In our case the knowledge base defines this puzzle based on Lord of the Rings with three predicates: before, next_to and fellowship_order. The before and next_to predicates express whether for two members in a list are before or next to each others respectively. The X, Y and List arguments expect variables (variable names are capitalized). The fellowship_order uses these predicates to express what is a valid, according to our logic puzzle, order of the members of the Fellowship. The members, such as legolas are atoms (they start with a lower case) and represent these characters in our domain.
The query, fellowship_order(Order). which was helpfully given to us by Chat-GPT, allows us to gather the valid orders according to the puzzle when querying the above knowledge base.
We can test this easily by entering the above Prolog code in the Tau Prolog sandbox. After pasting in the program, we can press consult program, which loads the knowledge base. As the goal that we want to query, we can enter fellowship_order(Order).. Doing this will retrieve Order = [legolas,gimli,frodo], which is a valid answer to the logic puzzle.
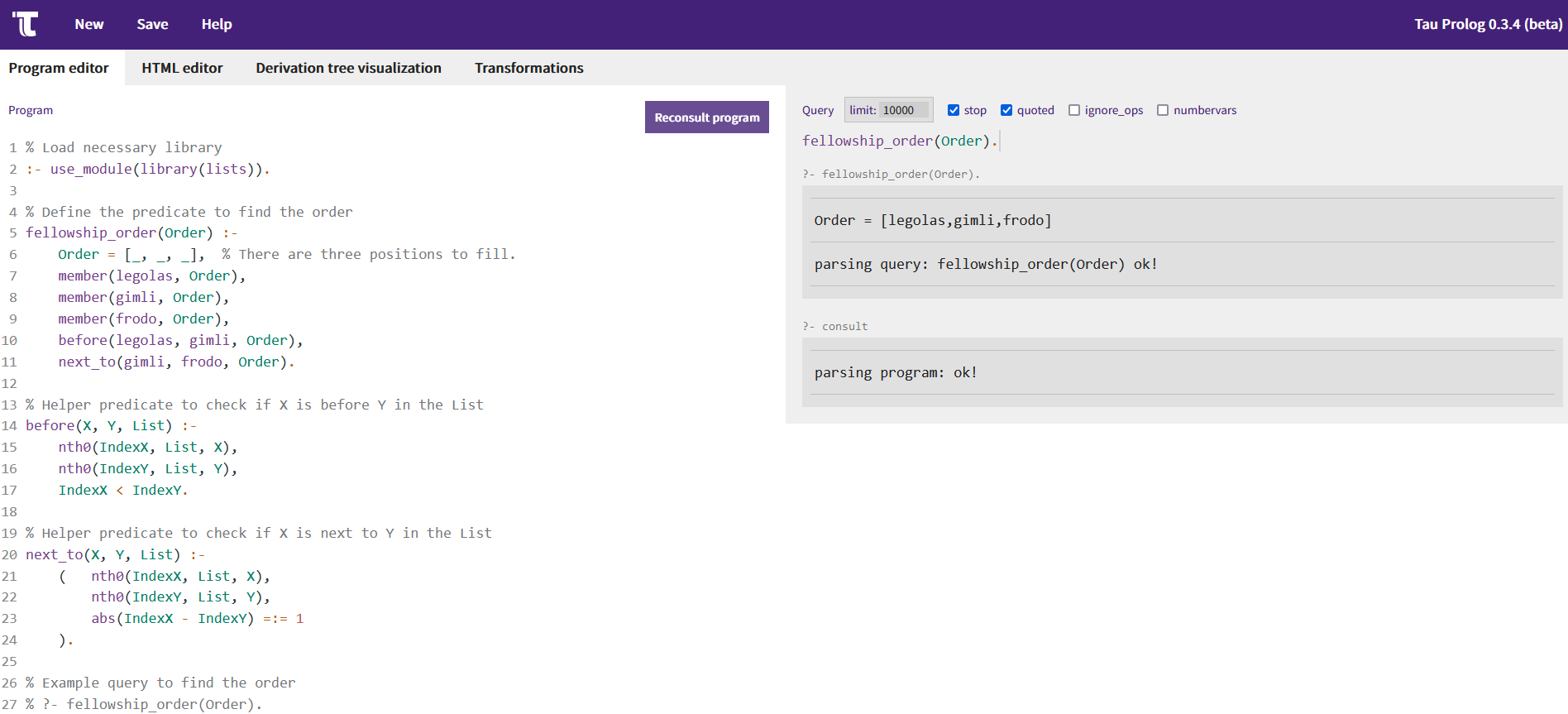
Consulting the short Prolog example of the logic puzzle.
Note that Order = [legolas,frodo,gimli] is a valid answer as well. If we would ask the query again in the Tau Prolog sandbox, we will get this answer instead. If we query for a third (or any subsequent) time, we get a false, which is Prolog's way of denoting that no answer could be found. This is due to Tau Prolog aiming to list all possible answers one by one given our query in this sandbox.
Now that we have gone over a small example, let's see if this approach can work with a larger puzzle. While we can ask for the full Prolog code for a larger puzzle, in the version of Chat-GPT used at the time of writing, it had some trouble giving us a full and complete working program with lots of restrictions. Instead we can take the small example and add new constraints to it.
Using this method we can create the following puzzle:
% Load necessary library
:- use_module(library(lists)).
fellowship_order(Order) :-
Order = [ _, _, _, _, _, _, _],
member(aragorn, Order),
member(frodo, Order),
member(sam, Order),
member(merry, Order),
member(pippin, Order),
member(gimli, Order),
member(legolas, Order),
% Defining relations based on problem statement
before(aragorn, pippin, Order), % Aragorn walks before Pippin.
hobbit_neighbor(frodo, Order), % Frodo walks next to at least another Hobbit.
hobbit_neighbor(sam, Order), % Sam walks next to at least another Hobbit.
before(gimli, legolas, Order), % Gimli walks ahead of Legolas.
next_to(merry, pippin, Order), % Merry walks next to Pippin.
after(frodo, aragorn, Order). % Frodo walks after Aragorn.
% Check if X is before Y
before(X, Y, [X|T]) :-
member(Y, T).
before(X, Y, [_|T]) :-
before(X, Y, T).
% Check if X is after Y
after(X, Y, List) :-
before(Y, X, List).
% Ensure Sam is next to another hobbit
hobbit_neighbor(X, List) :-
next_to(X, frodo, List);
next_to(X, sam, List);
next_to(X, merry, List);
next_to(X, pippin, List).
% Check if X is next to Y
next_to(X, Y, [X, Y|_]).
next_to(X, Y, [Y, X|_]).
next_to(X, Y, [_|T]) :-
next_to(X, Y, T).
% Example query to find the order
% ?- fellowship_order(Order).
This puzzle has a number of new types of restrictions and more members of the Fellowship represent, but works the same way as the previous one. If we run it in the sandbox we can get an answer such as Order = [aragorn,frodo,sam,merry,pippin,gimli,legolas] being returned. With an LLM we can even reverse the puzzle creation and get a textual description of the restrictions in the puzzle, as well as the puzzle itself. The following is the answer that ChatGPT returns when asked to describe the above puzzle in words:
Such an approach can give us a very interactive way to evolve our problem description as well as the solution. We can give a text description of new constraints to the LLM, play around with the generated code in the sandbox, and go back to the LLM to refine the descriptions of the problem until we have the right problem statement and the solution.
In this case the back and forth between the Prolog code and the text can help us further refine the puzzle. A helpful hint if one wants to experiment further: increasing the limit parameter that controls a maximum number of inferences can help to run more complex puzzles in the sandbox. Feel free to try it out with the sandbox!
I hope you enjoyed this journey into Prolog from LLMs and back again and will consider using Prolog in such a way during your quest to solve other problems as well!